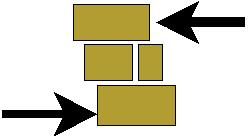
Gaudi's models

Why Gaudi realized one of Viollet le Duc's ideals

Viollet le Duc thought that shape (i.e. structure) should be adapted to the materials used. He appraciated gothic architecture as the most effective technic ever found to build stone cathedrals (large, high and lighty building). Gaudi founded a way even more effective for stone constructions. His way can be considered as the most effective way using some physical properties (it minimizes the shearing forces which are the causes of collapses). He found the way not using math as I will to demonstrate what I do assess but models that took naturally the optimum shape by putting them upside down. As you know it, Gaudi was very fond of nature and nature inspires his work very much. Once again natural shapes have proven to be effective and tightly linked to efficient structures.

Gaudi used models in several buildings including the Colegio Teresiano, The Guell crypt, the Sagrada Familia (only towers have been built so the "parabolic" structure is not visible). The "parabolic" archs are used in almost every building by Gaudi.

Comparison between stone works and chains

Stone works have two main caracteristics: a high resistance to a force of compression and a low resistance to a shearing force. The following drawings show a compression force on a stone column, a shearing force and the ultimate result of a shearing force.

Stone works structures and forces: From left to right: a) compression forces, b) effect of strong shearing forces, c) ultimate effects of shearing forces: the break down

A stone work structure with no shearing forces is safe. The more shearings there are, the more likely the structure will fall.

Chains have a high resitance to an extension force. And a nul resistance to a shearing force i.e. if you apply a shearing force at the extremities of a chain, the chain does not resist and the chain changes of shape in order to have only extension force.

Chains and forces: From left to right a)extension forces, b)shearing forces, c) and d) immediate effects of shearing forces
You can then define a transformation between chains structures and stone work structures with no shearing force (i.e. safe). It transforms extension into compression.

Gaudi's models

Gaudi used some models to test his structures. I have seen few pictures of them but I have never read any description of there fabrication. I have some ideas about it and I will try to explain how Gaudi or anyone else could have "calculate" a safe large stone structure without any computer.
Take chains with little link, glue, a large board. That's all. Oh, I was forgotten that you need not to be on the space shuttle. Just stay on earth, it will be easier than on the moon.
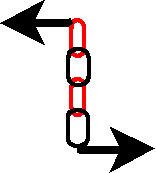
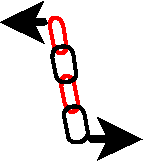
The trick to change compression into extension is to use gravity force. It is to put the stone work structure upside down to obtain a chain structure and reciprocally.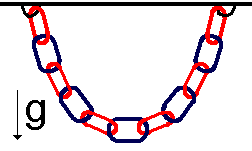

How can a "pseudo parabolic" arch be a "naturally efficient" structure for stone work

It is the first exercise with our model, making the simplest stone structure: an arch. Take a chain with small links and glue its two extremities to your bedroom ceiling (it works also in your bathroom). You will find thanks to our transformation above (i.e. downside up) an optimal shape for your arch. Playing with the length of the chain, and the distance between the two extremities, you can obtain different shapes for arches.

These chains shapes are in fact not parabolic but hyperbolical cosinus shapes, I don't know if there is an adjective for it so I will call it pseudo parabolic. If you are interested, you can read the demonstration below. This demonstration requires basic knowledge in physics (equilibrium laws) and 1st to 2nd year highschool in math (tangente, curve absice, differential equations). I have tried to go into deep detail so someone without this knowledge could understand (with derivative knowledge only). (deep detail but not rigorous details, sorry for math fanatics).

The system is constitued by the ceiling (an horizontal plan named P), Two glue points G and G' that belong to P, and a chain with "very little links" that is glued by its two extremities to G and G'. $l$ is the curve absice of the chain, $m$ _l is the linear mass. The system has two orthogonal symetry plans which are $P 1$ (the set of points at equidistance of the two glue points G and G') and P2 (the spawn(ed?) by $GG'$ and $g$ , and at home it's the plan of your computer screen). Of these considerations of symetry, We can conclude that the solution is also include in the plan P2 (i.e. your screen) and is symetrical by the mediatrice of [GG'] (i.e. the vertical line going by the middle of GG'). Two axes: horizontal ox, vertical oy with their associated unity vectors $i$ and $j . Say the
length of a link is dl so its mass is m$ _l dl. An intersting choice is to take the origine of the axes at the middle of the chain (which makes oy be the mediatrice because of the symetry of the solution.). this origine is also the 0 of the curviline absice. F(l) is the force that each link applies on its left neighbour at l abcice: therefore, F(l) is oriented from left to right. The force applied by a link to its right neighbour is -F(l) because the system is stable. (action-reaction law).

Let us consider the subsystem of the chain between -l and l. This system is also symetrical and immobile. We can apply to it the law of the equilibrium of forces. gravity P=-2lm_lgj, F(l)=F_x(l)i+F_y(l)j and F(-l)=F_x(-l)i+F_y(-l)j. Projecting on the axe oy, we get the equation: -F_y(-l)+F_y(l)-2lmg=0. We can add for symetry reasons that F_y(l)=-F_y(-l) so the equation becomes 2Fy(l)=2lmg that is F_y(l)=lm_lg.

Let us now consider the sub system composed of only one link. It is still in equilibrium so on ox axe we get F_x(l)-F_x(l+dl)=0 i.e. F_x(l)=Fx(l+dl) from link to link, we have F_x(l)=C1 whatever the value of l.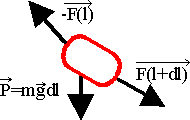

As the link is small, the tangente at point P(l) (called T(l)) is colinear to F(l). So we can write the definition of colinearity between T(l) and F(l):

(1) y'(x)=dy/dx=C2*m_lgl/C1

We now aim at eliminating l in function of y and x. We will use the Pytagorus theorem dl²=dx²+dy². This leads to dl/dx=sqrt(dy/dx²+1). We can derive (1): y''(x)=C2/C1*mgdl/dx and use the expression of dl/dx to give

(2): y''(x)=C3*sqrt(dy/dx²+1)

We will now make a variable change: we can assume that a function t exists where y'(x)=sh(t(x)) (sh is the hyperbolic sinus). That implies y''(x)=t'(x)ch(t(x)) applying the drivation law for conpouded functions. (2) can be rewrote as

(3) t'(x)ch(t(x))=C3*sqrt(sh²(t(x))+1)

Now let us use the relationship between sh and ch: ch²-sh² =1. we get

(4) t'(x)=C3

so t(x)=C3*x+C4 and replacing t in (3)

(5) y'(x)=sh(C3*x+C4)

Finally y(x)=C5*ch(C3*x+C4)/C3. And because y(0)=0 we can calculate that C4=0. So

y(x)=K*ch(C3*x)

where K=C5/C3.

Notes and Definitions:
sqrt is the square root.
Pytagorus theorem says that in a rectangle triangle, the square of the hypothenuse is equal to the sum of the squares of the two others "cotes"
sh is the hyperbolic sinus. Here are two equivalent definitions: 1) sh(x) is the odd part of e^x, 2) sh(x)=(e^x- e^-x)/2. It is called sinus because most of the trigonometrical formulas can be derived into sh and ch formulas. This is due to the fact that sin(x) is the imaginate part of e^ix.
ch is the hyperbolic cosinus. Here are two equivalent definitions: 1) ch(x) is the even part of e^x, 2) ch(x)=(e^x+ e^-x)/2. It is called cosinus because most of the trigonometrical formulas can be derived into sh and ch formulas. This is due to the fact that cos(x) is the real part of e^ix.

Generalization to take into account filling walls

The former calculus took into account only the structure. It is possible to take into account also the filling walls. It is to change the link mass from m_l g dl into m_l g dl+m_wy where m_w is the mass per surface unit of the wall. This modifies (1) into

(1') y'(x)=dy/dx=C2*m_lgl/C1+C2*m_wy/C1

I do not know how to solve simply those kind of differential equation but Gaudi knew how to do it without math: he evaluated the mass of the wall and then hang some little weights to the links to simulate the weight of the walls.

I hope you had fun in reading this.

Gaudi's models

Why Gaudi realized one of Viollet le Duc's ideals

Comparison between stone works and chains

Gaudi's models

How can a "pseudo parabolic" arch be a "naturally efficient" structure for stone work

Notes and Definitions:

Generalization to take into account filling walls